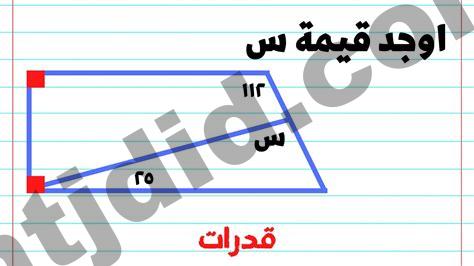
يسمى الشكل المجاور. الإجابة الصحيحة هي : شکل ثمانى.
الشكل المجاور
الأشكال الهندسية هي اللبنات الأساسية للهندسة. لكل شكل فريد من خصائصه وصفاته التي تميزه عن الأشكال الأخرى. وفي هذا المقال، سوف نستكشف بالتفصيل شكلًا هندسيًا شائعًا يُعرف باسم الشكل المجاور.
تعريف الشكل المجاور
الشكل المجاور هو مضلع مسطح مكون من أربعة أضلاع متساوية الطول و أربع زوايا قائمة. و بعبارة أخرى، هو مربع أو مستطيل، حيث يتساوي طول الضلعين المتقابلين، وتكون جميع الزوايا متساوية القياس وقائمة.
خصائص الشكل المجاور
عدد الأضلاع: 4
عدد الزوايا: 4
قياس الزوايا: جميعها قائمة (90 درجة)
الأضلاع: متساوية الطول
القطران: متعامدان وينصفان بعضهما البعض
المساحة: أ = ض ض حيث ض هو طول الضلع
المحيط: م = 4 ض
أنواع الشكل المجاور
هناك نوعان رئيسيان من الأشكال المجاورة:
المربع: شكل مجاور منتظم له جميع الأضلاع متساوية الطول و جميع الزوايا قائمة.
المستطيل: شكل مجاور غير منتظم له ضلعان متقابلان متساويان في الطول، والضلعان الآخران متساويان في الطول، و جميع الزوايا قائمة.
استخدامات الشكل المجاور
للشكل المجاور تطبيقات واسعة في مجالات مختلفة، منها:
الهندسة المعمارية والبناء: أساس العديد من الهياكل والمباني
الرياضيات: مثال على المضلع المنتظم والمستطيل
الفيزياء: نموذج للكثير من الأجسام ذات الوجوه المستوية
الحوسبة: أساس وحدات البكسل في الشاشات الرقمية
الإنشاء الهندسي للشكل المجاور
هناك طريقتان رئيسيتان لإنشاء شكل مجاور هندسيًا:
الطريقة الأولى: رسم مربع بزاوية قائمة، ثم رسم خطين متعامدين من منتصف كل ضلع إلى الضلع المقابل.
الطريقة الثانية: رسم مستطيل بأضلاع متقابلة متساوية الطول، ثم رسم خطين متعامدين من منتصف كل ضلع إلى الضلع المقابل.
إثبات خصائص الشكل المجاور
يمكن إثبات خصائص الشكل المجاور باستخدام مبادئ الهندسة الإقليدية:
تساوي جميع الأضلاع: في المربع، يمكن إثبات ذلك باستخدام مبرهنة فيثاغورس. في المستطيل، يمكن إثبات ذلك باستخدام مبرهنة المتطابقات.
تساوي جميع الزوايا: يمكن إثبات ذلك باستخدام مبرهنة فيثاغورس.
تعامد القطرين: يمكن إثبات ذلك باستخدام مبرهنة المتطابقات.
الشكل المجاور هو شكل هندسي أساسي ذو خصائص مهمة واستخدامات واسعة. سواء كان مربعًا منتظمًا أو مستطيلًا غير منتظم، فإن الشكل المجاور يلعب دورًا مهمًا في العديد من المجالات، من الهندسة إلى الفيزياء إلى الحوسبة.